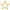Soluzione del test: Calze della befana
Calze della befana
La Befana ha portato 8 piccoli pacchetti regalo per 8 fratelli. I pacchetti sono tutti assolutamente identici alla vista ma Gianprimo sostiene che uno di questi pacchetti è più pesante e spetta a lui in quanto primogenito.
Giansecondo prova a sollevare i pacchetti uno per volta ma non trova differenze sensibili. Gianterzo e Gianquarto fanno lo stesso e concordano con Giansecondo.
Sono tutti ansiosi di vedere i regali della Befana ma sono bloccati in questa situazione.
Giannottavo, il più piccolo, propone una soluzione: prendere la bilancia a 2 piatti del nonno Gianni e pesare tutti i pacchetti, ma il più pesante potrà aggiudicarselo solo chi riuscirà a individuarlo con il minor numero di pesate.
Qual è quindi il minor numero di pesate da effetturare? E come fare per individuare il regalo più pesante?
SOLUZIONE
Il numero minimo di pesate è 2.
Ecco come fare.
I pacchetti sono 8 e li divido in 3 gruppi: due gruppi da 3 pacchetti e un gruppo da 2 pacchetti.
(Prima pesata) Peso la prima terna con la seconda terna: se la bilancia è in equilibrio vuol dire che il pacchetto più pesante è nella coppia non pesata e quindi ponendo uno per piatto i due pacchetti della coppia posso determinare il più pesante (con la seconda pesata).
Se invece alla prima pesata uno dei due piatti pende, significa che il pacchetto che sto cercando è in quella terna. Per individuare quale dei tre pacchetti pesa di più ne pongo due a caso sui piatti (seconda pesata) e uno lo tengo da parte. Se la bilancia è in equilibrio allora il più pesante è quello tenuto da parte, altrimenti la bilancia mi indicherà esattamente il pacchetto più pesante.
Giuseppe Valloire è stato il primo (alle 10:49) ad aver scritto la soluzione (sufficientemente dettagliata) sulla nostra pagina Facebook ed ha vinto il seguente libro:
- Si fa presto a dire mamma (libro autografato, con dedica personale da parte dell'autrice)
Leggi sulla nostra home page quando ci sarà il prossimo indovinello a premi